問題
問題
白玉1個、赤玉2個、青玉4個、黄玉6個をすべて糸でつないでネックレスを作る。
何種類のネックレスができるか。
これは見た目よりもはるかに難しい問題です。
まずは順を追って、例題を何題か解くところから始めましょう。
例題１
問題
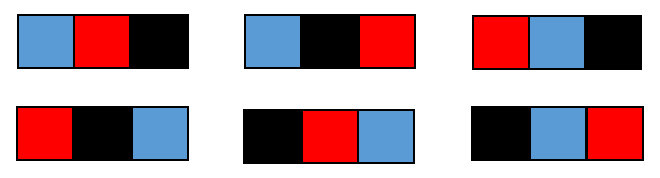
(図１)の3つのブロックをつなげて1本の棒をつくる。
何種類の棒できるか。
(図１）
これは簡単です！3通りです！
↑こんな感じで3!=6通りの並べ方がありますが、左右対称の棒は同じものなので、2で割って3通りです。
その通り。次の問題に行きましょう。
例題２
問題
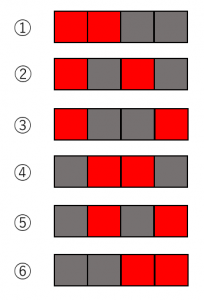
図2の4つのブロックをつなげて1本の棒をつくる。
何種類の棒できるか。
（図２）
さっきと同じで、左右対称のものを気にせずに一列に並べると $\dfrac{4!}{2!2!}$ 通りですが、それを2で割ったらいいんじゃないですか？
いや、2で割るのはやりすぎなんです。
えっ？やりすぎ…？
まずは書き上げてみましょう。
この6種類ですね。
この中で、回転させれば同じになるものが混ざっていますね。何番と何番ですか？
①と⑥は同じですね。あと②と⑤も！
もうないですか？
もうないですね…
ですね。③や④は、回転して同じになる組はありません。
というわけで、棒の作り方は何通りありますか？
「①⑥」と、「②⑤」、③と④で、4通りですね。
式にすると、$\left(\dfrac{4!}{2!2!}-2\right)\div2+2=4$
で4通りです。
えっ、この式は…!?
回転させて同じものがあるので、基本的には2で割りたいのです。しかし、左右対称である③と④の2つは2で割ることができません。
だから一旦その2つを避けて割って、後からその2つを足したのです。
$$\left(\dfrac{4!}{2!2!}-2\right)\div2$$
これが③と④を避けて割った…
それに後から③と④を足して…
$$\left(\dfrac{4!}{2!2!}-2\right)\div2+2$$
なるほど確かに…!
求める場合の数は、
$\left(\dfrac{4!}{2!2!}-2\right)\div2+2=4$（通り）
例題３
問題
異なる5つの玉をつないでネックレスを作る。何種類のネックレスができるか。
これは普通の「じゅず順列」ですね！
裏返して同じものができるから、
$4!÷2=12$（通り）
です！これは簡単！
OKです。
問題 再び
ようやく本題です。改めてこの問題を考えてください。
問題
白玉1個、赤玉2個、青玉4個、黄玉6個をすべて糸でつないでネックレスを作る。何種類のネックレスができるか。
白玉が1個だけなので白玉を固定して…
のこりの並べ方は $\dfrac{12!}{2!4!6!}=13860$（通り）で…
これを2で割る…ではダメなんですね？
基本は2で割りたいのです。たとえばこんなもの↓が2つセットになるので、基本的には2で割りたいのです。
裏返して同じものだから２で割るんですね！
しかし、割ってはいけないものもあります。
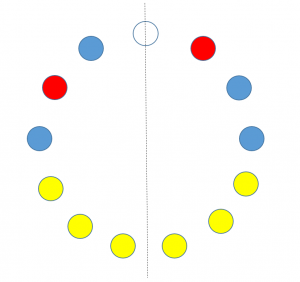
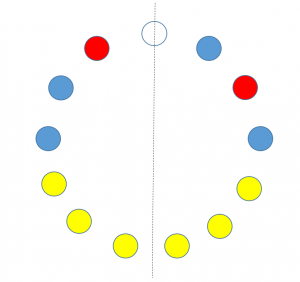
先ほどの例を思い出してください。
…左右対称だと割れない…
そうです。↑こんなやつです。
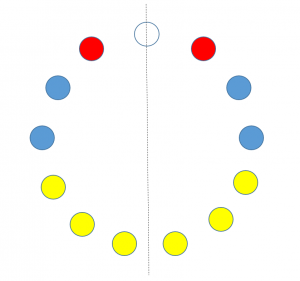
左右対称であるのは何通りありますか？
右側に赤玉1個、青玉2個、黄玉3個を並べたら、左側は決まるから…
$\dfrac{6!}{2!3!}=60$ (通り)
では、最終的な答えを求めてください。
避けて、割って、足す…
$\left(13860-60\right)\div2+60=6960$
6960通りです！
