2つの図形の交点を通る図形
2つの図形の交点を通る図形

$f(x,y)+k\cdot g(x,y)=0$
が表す図形は、実数定数 $k$ の値に係わらず、2つの図形
$f(x,y)=0$ と $g(x,y)=0$ の交点を通る。
※スマホの場合、横向きを推奨














































具体例でまずは意味から理解しましょう。
具体例









































$(x+y-2)+k(x-y)=0$
が表す図形は、実数定数 $k$ の値に係わらず、2つの図形
$x+y-2=0$ , $x-y=0$
の交点を通る。














































意味が分かるところから考えていきましょう。























$2$ 本の直線の交点なので、$(1,1)$ です!
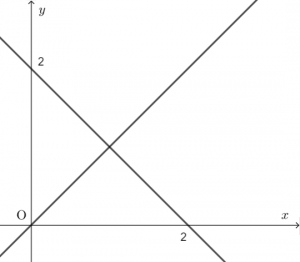










































































































次に $(x+y-2)+k(x-y)=0$ ですが、$k$ に色々な値を入れて、図形がどう変わるかを考えましょう。
例えば $k=0$ とするとどうなりますか?























































































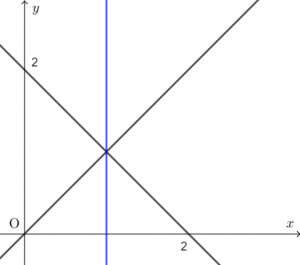

































































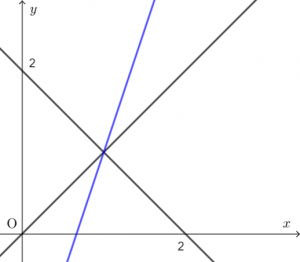

































































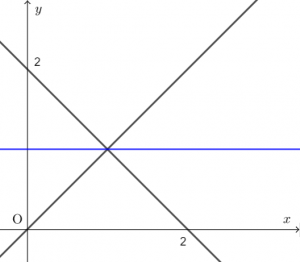

























































































$(x+y-2)+k(x-y)=0$
が表す図形は、実数定数 $k$ の値を色々変えると様々な直線に変わるが、
どのような $k$ の値を入れても、2つの図形
$x+y-2=0$ , $x-y=0$
の交点、すなわち $(1,1)$ を通る。






























































































グラフがある点を通るのは、方程式が成り立つとき、つまりその座標を $x,y$ に代入して成立するときです。
ここまでは大丈夫ですか?
































































$x+y-2=0$ と $x-y=0$ どちらに入れても等式を成立させる。これもOKですか?





























































































$0+k\cdot0=0$ になって、絶対に成立します…!









































































































$(x+y-2)+k(x-y)=0$
が表す図形は、実数定数 $k$ の値に係わらず、2つの図形
$x+y-2=0$ と $x-y=0$
の交点を通る。









































































































$f(x,y)+k\cdot g(x,y)=0$
が表す図形は、実数定数 $k$ の値に係わらず、2つの図形
$f(x,y)=0$ と $g(x,y)=0$ の交点を通る。
































































問題
$x^{2}+y^{2}=4$ と $x^{2}+y^{2}-2x-4y+3=0$ の $2$ つの交点をA,Bとする。
(1) 直線ABの方程式を求めよ。
(2) 点A,Bと $(3,0)$ を通る円の方程式を求めよ。



















































































































(1)の解答









































$f(x,y)+k\cdot g(x,y)=0$
が表す図形は、実数定数 $k$ の値に係わらず、2つの図形
$f(x,y)=0$ と $g(x,y)=0$ の交点を通る。









































$(x^{2}+y^{2}-4)+k(x^{2}+y^{2}-2x-4y+3)=0$
が表す図形は、実数定数 $k$ の値に係わらず
$x^{2}+y^{2}-4=0$ と
$x^{2}+y^{2}-2x-4y+3=0$ の交点(すなわちA、B)を通る。
































































はい。$f(x,y)$ を $x^{2}+y^{2}-4$ と、
$g(x,y)$ を $x^{2}+y^{2}-2x-4y+3$ と読み替えたらいいですね!









































では $(x^{2}+y^{2}-4)+k(x^{2}+y^{2}-2x-4y+3)=0$ の $k$ の値を変えていくと、どんな図形を表すか分かりますか?





























































































































































円じゃない…









































$x^2$ や $y^2$ があったら直線にはなりませんが…























$x^2$ と $y^2$ が消えたときは直線になります!









































































































$(x^{2}+y^{2}-4)+(-1)(x^{2}+y^{2}-2x-4y+3)=0$
$-4+2x+4y-3=0$
$2x+4y-7=0$ …(答)









































(2)の解答









































$(x^{2}+y^{2}-4)+k(x^{2}+y^{2}-2x-4y+3)=0$









































この方程式が表す図形は、$k$ の値に係わらず、
$x^{2}+y^{2}-4=0$
$x^{2}+y^{2}-2x-4y+3=0$
































































$k$ を色々変えると色々な円(たまに直線)になって、それらはすべてA、Bを通る…
































































$(x^{2}+y^{2}-4)+k(x^{2}+y^{2}-2x-4y+3)=0$ に $(3,0)$ を代入して…
$5+k\cdot6=0$
$k=-\dfrac{5}{6}$
































































$(x^{2}+y^{2}-4)-\dfrac{5}{6}(x^{2}+y^{2}-2x-4y+3)=0$









































$6(x^{2}+y^{2}-4)-5(x^{2}+y^{2}-2x-4y+3)=0$
$6x^{2}+6y^{2}-24-5x^{2}-5y^{2}+10x+20y-15=0$
$x^{2}+y^{2}+10x+20y-39=0$ …(答)









































答案









































(1)
$(x^{2}+y^{2}-4)+k(x^{2}+y^{2}-2x-4y+3)=0$
が表す図形は、実数定数 $k$ の値に係わらず
$x^{2}+y^{2}-4=0$
$x^{2}+y^{2}-2x-4y+3=0$ の交点を通る。
$k=-1$ のとき,
$(x^{2}+y^{2}-4)+(-1)(x^{2}+y^{2}-2x-4y+3)=0$
$-4+2x+4y-3=0$
$2x+4y-7=0$
となり,この図形は直線を表し,A,Bを通るから,これは直線ABの方程式である。
(2)
$(x^{2}+y^{2}-4)+k(x^{2}+y^{2}-2x-4y+3)=0$ が $(3,0)$ を通るから,
$5+k\cdot6=0$
$k=-\dfrac{5}{6}$
このとき,
$(x^{2}+y^{2}-4)-\dfrac{5}{6}(x^{2}+y^{2}-2x-4y+3)=0$
$6(x^{2}+y^{2}-4)-5(x^{2}+y^{2}-2x-4y+3)=0$
$6x^{2}+6y^{2}-24-5x^{2}-5y^{2}+10x+20y-15=0$
$x^{2}+y^{2}+10x+20y-39=0$
この図形は円を表し,3点A,B,(3,0)を通るので,これは求める円の方程式である。
📘[記事がわかりやすいと感じた方へ ]
記事の執筆者は、数学・物理を中心にオンライン個別指導を行っています。
個別指導でも、記事のような考え方でやり取りを重視しながら進めています。
✑概要をみる(➡指導システム)





