直線の通過領域
e-yobi管理者 榊原
直線の通過領域

今日は直線の通過領域について基本から学習します。



あっ、これ難しいやつ…
問題
問題
$t$ を実数とする。直線 $l:y=-2(t+1)x+t^{2}+1$ について、次の問いに答えよ。
(1) $l$ が $(0,1)$ を通るような実数 $t$ の値を求めよ。
(2) $l$ が $(-2,1)$ を通るような実数 $t$ が存在するかを調べよ。
(3) $t$ が実数全体を動くとき、$l$ の通過する領域を図示せよ。




















今回は誘導付きで丁寧に小問を付けていますが、実際は(3)のみがあるのが普通です。
















(3)はよくわからないですが、(1)(2)は普通にいけそうです!
(1)の解答
















(0,1)を通るから、$y=-2(t+1)x+t^{2}+1$ に $(0,1)$ を代入して…
$1=0+t^{2}+1$
$t^{2}=0$
















$t=0$ です!




















OKです。念のため、問題の設定を確認しておきます。
$t$ の値を色々変えると、直線は様々に変わります。
例えば $t=-2$ とするとこう。
$y=2x+5$
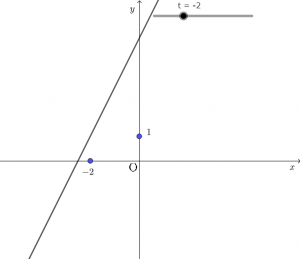





















$t=3$ とするとこう。
$y=-8x+10$
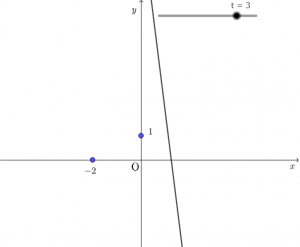





















$t=0$ とするとこう。
$y=-2x+1$
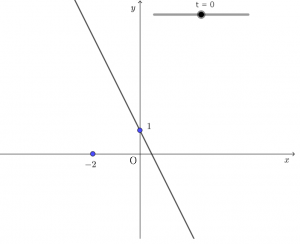

















確かに $t=0$ のときに $(0,1)$ を通っていますね!
(2)の解答
















$(-2,0)$ を通るとすると、$y=-2(t+1)x+t^{2}+1$ に $(-2,0)$ を代入して…
$0=-2(t+1)(-2)+t^{2}+1$
$t^{2}+4t+5=0$




これを解くと…
…いや、解けないですね。




















「解けない」とはこの場合どういう意味ですか?
















あ、実数解をもたないということです。




















どうやって判断できましたか?
















判別式から、
$D=4^{2}-4\cdot5<0$
だからです!




















そのとおりですね。
















ということで、$(-2,1)$ を通るような実数 $t$ は存在しない、です!
(3)の解答




















さて、ここまで来ると(3)の意味が理解できますか?
直線が通過する領域を調べるとは、直線が通るか通らないかを調べるということです。
















つまり、$D$ が $0$ 以上かどうかを調べる、ということですね!




















そういうことです。
$y=-2(t+1)x+t^{2}+1$ が、ある点 $(x,y)$ を通るかどうかを調べましょう。
















$(-2,1)$ を通るかなら、$(x,y)$ に $(-2,1)$ を代入して考えたので…




















$(x,y)$ に $(x,y)$ を代入して考えるのです。



$(x,y)$ に $(x,y)$ を代入…?




















代入している $(x,y)$ は、$y=-2(t+1)x+t^{2}+1$ の式の上の $x,y$ とは別のものということに注意が必要ですね。
直線が点 $(-2,1)$ を通るかを調べるのと同様に、直線が点 $(x,y)$ を通るかを調べるのです。




なるほど…
















代入すると $y=-2(t+1)x+t^{2}+1$ となって…
(見かけ上なにも変わらないけど、代入している…)




















そのあとは判別式を考えましたね。$t$ の $2$ 次方程式だと見たのです。
















ということは、$t$ について整理して…
$t^{2}-2xt-2x-y+1=0$
















この判別式が $0$ 以上なら、実数解があるということですね。




















ということはつまり…
















$t$ を色々動かしたうちのどこかの実数 $t$ のときに、点 $(x,y)$ を通るということです!
$\dfrac{D}{4}=x^{2}-(-2x-y+1)≧0$
$y≧x^{2}+2x-1$
$y≧\left(x+1\right)^{2}+2$




















この条件をみたす $(x,y)$ が、直線がいずれかの $t$ で通る点、ということになります。
求める領域は図の灰色部。境界線を含む。
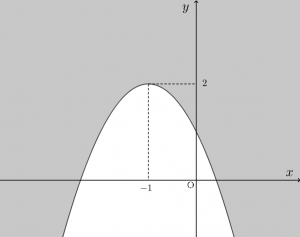





















ちなみにですが、$t$ を色々かえた直線をたくさんかくと、下のようになります。
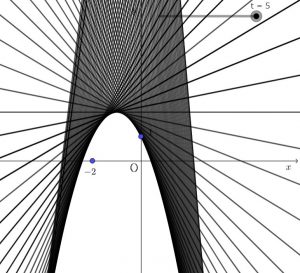





















これは-5から5まで0.1刻みで直線をかいたものです。もっと細かく、広くとれば領域全体が塗りつぶされるようになります。
















確かに通る領域はあっていそうですね!




















とりあえずここまでが通過領域の基本です。




$(x,y)$ は実は代入している…
ここが難しいですね…




















少し難易度が高い問題はまたの機会に。
📘[記事がわかりやすいと感じた方へ ]記事の執筆者は、数学・物理を中心にオンライン個別指導を行っています。
個別指導でも、記事のような考え方でやり取りを重視しながら進めています。✑概要をみる(➡指導システム)
個別指導でも、記事のような考え方でやり取りを重視しながら進めています。✑概要をみる(➡指導システム)
ABOUT ME
e-yobi管理者 榊原
本ブログでは、私の指導スタイルの参考になるものを発信しています。学習に関するお悩み解決に、私の指導が合いそうと感じられた方はぜひ一度ご相談ください➡授業の概要はこちら





