三角関数の合成

三角関数の合成は学校で習っていて、合成する方法は知っているんですが、仕組みがよくわかっていないんです。
順を追って教えてもらうことはできますか?








加法定理を逆算する
まずは原理原則から考えていくので、結構難しくなります。













加法定理により、例えば
$\sin\left(x+\dfrac{\pi}{3}\right)$
$=\dfrac{1}{2}\sin x+\dfrac{\sqrt{3}}{2}\cos x$
となるのは分かりますね?
これを逆算するのを合成と言います。




















(右辺)=$\dfrac{1}{2}\sin x+\dfrac{\sqrt{3}}{2}\cos x$
を先に見せられて、もともとが
(左辺)=$\sin\left(x+\dfrac{\pi}{3}\right)$
であったことを逆算するのです。




















まずは
$\dfrac{1}{2}$$\sin x+$$\dfrac{\sqrt{3}}{2}$$\cos x$
と、加法定理から$\sin(x+\alpha)$を展開した
$\sin x$$\cos\alpha$$+\cos x$$\sin\alpha$
とを見比べて、
$\cos\alpha=\dfrac{1}{2}$
$\sin\alpha=\dfrac{\sqrt{3}}{2}$
となる角を探します。このような $\alpha$ は見つかりますか?



















というわけで
$\dfrac{1}{2}\sin x+\dfrac{\sqrt{3}}{2}\cos x$
$=\sin x\cos\dfrac{\pi}{3}+\cos x\sin\dfrac{\pi}{3}$
となって、
$\dfrac{1}{2}\sin x+\dfrac{\sqrt{3}}{2}\cos x=\sin\left(x+\dfrac{\pi}{3}\right)$
と合成できるのです。






係数をくくりだす













$\sin x+\sqrt{3}\cos x$
をこのまま
$\cos\alpha=1$
$\sin\alpha=\sqrt{3}$
としてもそんな角はありません。
そこでいったん2をくくりだして
$2\left(\dfrac{1}{2}\sin x+\dfrac{\sqrt{3}}{2}\cos x\right)$
とすれば先ほどと同じことができるようになり、
$2\sin\left(x+\dfrac{\pi}{3}\right)$
と合成されます。




















$\sin^{2}\alpha+\cos^{2}\alpha=1$ をみたすようににくくりだしました。
1 と $\sqrt{3}$ のままでは $1^{2}+\sqrt{3}^{2}=4$
となって、$\sin^{2}\alpha+\cos^{2}\alpha=1$ を満たさなくなってしまいます。
右辺を1にするために両辺を4で割ると $\left(\dfrac{1}{2}\right)^{2}+\left(\dfrac{\sqrt{3}}{2}\right)^{2}=1$ となりますから、2で割れば $\sin^{2}\alpha+\cos^{2}\alpha=1$ が成立すると分かります。






形式的な合成手順













$\sin x+\sqrt{3}\cos x$ の合成をもう少し機械的にやることを考えましょう。
はじめは理由をしっかり考えながらゆっくり進めていきます。
まず、くくりだす数 $r$ が何かは分からないとしておいて、いったん
$r\left(\dfrac{1}{r}\sin x+\dfrac{\sqrt{3}}{r}\cos x\right)$
と変形します。
$\cos\alpha=\dfrac{1}{r}$,$\sin\alpha=\dfrac{\sqrt{3}}{r}$
となるわけですが、これは $\cos\alpha:\sin\alpha=1:\sqrt{3}$ であることを意味します。
$\cos\alpha$ が $x$ 座標
$\sin\alpha$ が $y$ 座標であることを考えて、$\alpha$ は図形的に
$\alpha=\dfrac{\pi}{3}$ と求めることができます。(下図)
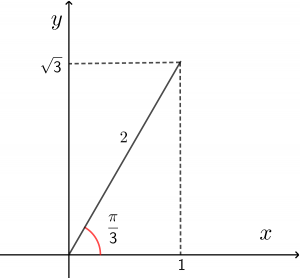

ところで、$\sin^{2}\alpha+\cos^{2}\alpha=1$を満たさねばいけませんから、$\left(\dfrac{1}{r}\right)^{2}+\left(\dfrac{\sqrt{3}}{r}\right)^{2}=1$
つまり、$r=\sqrt{1^{2}+\sqrt{3}^{2}}=2$ が分かります。




















分母の $r^{2}$ を払ってルートをとったんです。両辺に $r^{2}$ をかけると、$1^{2}+\sqrt{3}^{2}=r^2$ となりますから。
これは、$r$ が上の図の斜辺の長さであることを意味します。(三平方の定理より)
色々と理由を積み上げてきましたが、結局は上の図から読み取るだけで
$r=2$, $\alpha=\dfrac{\pi}{3}$ が分かり、
$2\left(\cos\dfrac{\pi}{3}\sin x+\sin\dfrac{\pi}{3}\cos x\right)$
と変形できることになって、
$2\sin\left(x+\dfrac{\pi}{3}\right)$
と合成できます。
以上の結果をすべて認めてしまって機械的に合成すると、
① $\alpha$ は $\cos\alpha:\sin\alpha=1:\sqrt{3}$ から求める
② $r$ は $\sqrt{1^{2}+\sqrt{3}^{2}}=2$、すなわち斜辺の長さから求める
という手順を踏むことになります。






よくある質問







































合成が使えるとき













「いつ合成したらいいんですか?」と聞かれることも多いです。
「いつ使ったらいいか」の代わりに、「いつなら使えるか」でお答えしておきましょう。
三角関数の合成が使えるのは、
① サイン,コサイン, どちらも1次である
② 角がそろっている(どちらも $\theta$ やどちらも $2\theta$ )
ことが条件です。






