$\cos\frac{\pi}{5}$の値の求め方|三角関数の関係式から導く
手順を覚えてしまうべき有名問題を紹介します。
※スマホの場合、横向きを推奨
問題
$x=\frac{\pi}{5}$ とする。
(1) $\sin3x=\sin2x$ が成り立つことを示せ。
(2) $\cos\frac{\pi}{5}$ の値を求めよ。
準有名角
例えば45°、60°は三角比の値をすぐに答えられる有名角です。
また75°などは加法定理を使えば三角比の値が求まる「準有名角」です。
そしてこの問題で扱う $\dfrac{\pi}{5}$ (72°)もまた、ちょっとした工夫で三角比の値が求まる準有名角です。
求めるための手順が「有名」ですので、しっかりと覚えてしまいましょう。
等式成立の証明

まずは(1) $\sin3x=\sin2x$ が成立することを示しましょう。
慣れていない人は、問題を解こうとして反射的に2倍角・3倍角の公式を使ってしまいがちですが、「中身を比べる」という方法も強力であることを忘れてはいけません。


「中身を比べる」とは…?











問題文から $5x=\pi$ がわかるので、$3x=\pi-2x$
よって公式 $\sin(\pi-x)=\sin x$ をつかえば、
$\sin3x=\sin(\pi-2x)=\sin2x$
となり、示された。






確かに公式を使えばそうなんですが、なんだかイメージがしにくいです…











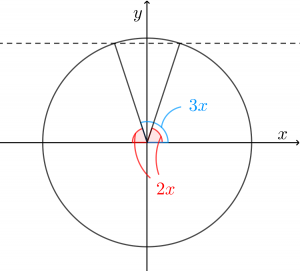












意外とこの部分が最大の難所かもしれませんね。
2次方程式への変換











「(2)$\cos\frac{\pi}{5}$ の値を求めよ。」
これを解くために、$\sin3x=\sin2x$ を2次方程式に変換します。






3倍角の公式を使うので、3乗が出てくると思うんですが…











2倍角・3倍角の公式より、
$\sin3x=\sin2x$ を変形すると
$3\sin x-4\sin^{3}x=2\sin x\cos x$















もう一度問題を見てみましょう。
求めないといけないのは$\cos$ ですね。ところができた式は$\sin$が入っています。困りました。

















$\sin x≠0$より、両辺を $\sin x$ で割ると
$3-4\sin^{2}x=2\cos x$

















計算を続けると、
$3-4(1-\cos^{2}x)=2\cos x$
$4\cos^{2}x-2\cos x-1=0$




$\cos\dfrac{\pi}{5}$ の値を求める
2次方程式を解いて、
$\cos x=\frac{1\pm\sqrt{5}}{4}$
ここで $x=\frac{\pi}{5}$ より $\cos x>0$ なので、
$\cos \frac{\pi}{5}=\frac{1+\sqrt{5}}{4}$ …解答終わり





















これは偶然ではなく必然なんです。$\cos$ のみの式になることは初めから分かっていたのです。
その理由は長くなるので、別の機会にお話ししましょう。(→「チェビシェフ多項式」)
📘[記事がわかりやすいと感じた方へ ]
記事の執筆者は、数学・物理を中心にオンライン個別指導を行っています。
個別指導でも、記事のような考え方でやり取りを重視しながら進めています。
✑概要をみる(➡指導システム)





