まずは次の因数分解をやってみましょう。
問題
(1) $2x^{2}-7x+3$
(2) $6x^{2}+19x+15$
(3) $24x^{2}+11x-18$
(4) $36x^{2}-3x-14$
(5) $72x^{2}-101x-48$
(1) $2x^{2}-7x+3=(2x-1)(x-3)$
(2) $6x^{2}+19x+15=(3x+5)(2x+3)$
(3) $24x^{2}+11x-18=(8x+9)(3x-2)$
その方法を使って(5)を自分でやってみてください。
素因数分解
(4) $36x^{2}-3x-14$ を因数分解してみましょう。
まずはじめに2乗の係数と定数項を素因数分解してみてください。
2乗の係数… $36=2^{2}×3^{2}$
定数項 … $14=2×7$
です。
これが第一のポイントです。素因数分解すると積の分かれ方がよく見えるようになりますから。
例えば14の分け方はどんなものがあり得ますか？
そうですね。
でも36は色々な分け方があって、一つ一つ考えるのは大変そうです。
実験をしながら特定していきましょう。
倍数に注目した絞り込み
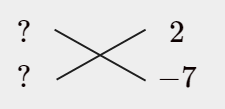
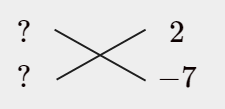
例えばこんな感じにしましょうか。
ここで、$36=2^{2}・3^{2}$ も上手く2つに配分するわけですが、例えば…
$(4x+2)(9x-7)$ と因数分解できるということですよ？
2をくくりだすと $2(2x+1)(9x-7)$
となって、どの項も係数が偶数でないとおかしくなってしまいます。
あっ、無理です！
ということは、3は上下2つに分けないといけないということですね。
例えばこんな感じなら…
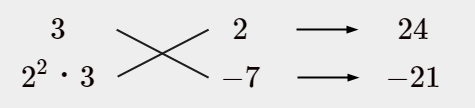
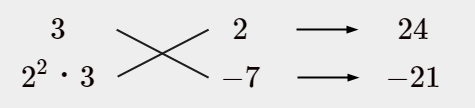
$24-21=3$
惜しい！
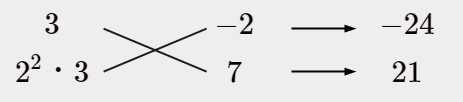
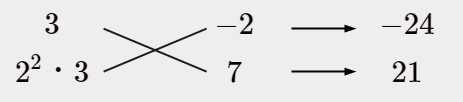
$36x^{2}-3x-14$
$=(3x-2)(12x+7)$ ……（答）
練習
(5) $72x^{2}-101x-48$
これに挑戦してもらいましょう。
まずは準備ですが、素因数分解すると…
$72=2^{3}・3^{2}$
$48=2^{4}・3$
さっきは「偶数であるか」「3の倍数であるか」に注目して特定しましたが、今回の101はどうでしょう。
まず、101は偶数ではありませんね。
101は3の倍数ですか？
これで準備はOKです。
さっきの要領で見つけることができますか？
101は偶数でも3の倍数でもないということは…
2も、3も上下に分けたらダメなんですね。
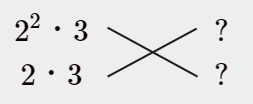
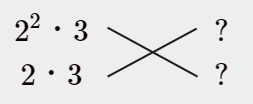
こういう分け方はダメ。
$2^{3}$ も $3^{2}$ もカタマリで動かさないといけないっていうことですね。
$2^{3}$
$3^{2}$
後ろの配分はこうでないとダメですね。
（だって、そうしないと2や3で全部がくくれてしまうから！）
あとはマイナスをどっちにつけるか…
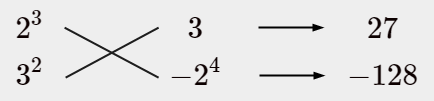
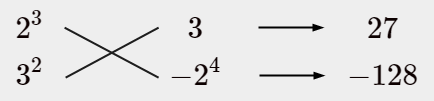
$72x^{2}-101x-48$
$=(8x+3)(9x-16)$ ……（答）
