対数関数の置換えによる最大値問題｜オンライン予備校 e-YOBI ネット塾

文字の置き換えによる基本的な解法を学びましょう。

問題

$x>1,y>1,xy^{2}=16$ のとき、 $(\log_{2}x^{2})(\log_{2}y)$ の最大値を求めよ。

指数関数や対数関数を一つの文字と置くのはよくある解法のパターンです。

解法1　まず置換え

({log}_{2} x^{2}) ({log}_{2} y)

$(\log_{2}x^{2})(\log_{2}y)$ の最大値を求めるわでですが、まず始めに置換えをしてみましょう。

$x>1,y>1$ において、

$(\log_{2}x^{2})(\log_{2}y)=(2\log_{2}x)(\log_{2}y)$

と書き換えられるので、

$\log_{2}x=X$

$\log_{2}y=Y$ と置くことで

$(\log_{2}x^{2})(\log_{2}y)=2XY$

となる。

置換えはできましたが、前半の条件

x > 1, y > 1, x y^{2} = 16

$x>1,y>1,xy^{2}=16$ はどうしましょう。

{log}_{2} x = X

$\log_{2}x=X$ ，

{log}_{2} y = Y

$\log_{2}y=Y$

と置いたわけですから、やるべき操作は決まってきます。

…両辺の対数をとる…！

$xy^{2}=16$ の両辺を底を $2$ とする対数をとって、

$\log_{2}xy^{2}=\log_{2}16$

$\log_{2}x+2\log_{2}y=4$

よって

$X+2Y=4$

と書き換えられる。

結局

「 $X+2Y=4$ のとき、 $2XY$ の最大値を求めよ。」

と書き換えられました。

ただし、よく言われるように「置換えたら範囲を考える」ことを忘れないでください。

「置き換えたら範囲」、よく言われます！

x > 1, y > 1

$x>1,y>1$ という条件をまだ使っていないですね。

$x>1$ より

$X=\log_{2}x>\log_{2}1=0$

よって $X>0$

$y>1$ より

$Y=\log_{2}y>\log_{2}1=0$

よって $Y>0$

置換えによって、

「 $X>0, Y>0, X+2Y=4$ のとき、

$2XY$ の最大値を求めよ。」

という問題に差し変わったことになります。

もう対数の問題ではなくなりましたね。

あとは…

2変数なので、1文字消去すればいいですね！

$X+2Y=4$ より

$X=4-2Y$

よって

$2XY=2(4-2Y)Y$

$=4(2-Y)Y$

これで

X

$X$ は消去できましたが、

Y

$Y$ には範囲がありましたね。

Y > 0

$Y>0$ でしたね。

さらに

Y

$Y$ の条件だけでなく、

X > 0

$X>0$ という条件もありましたね。

$X$ の条件も考えないといけないわけですが、 $X$ は消去してしまいました。

あっ…

「置換をしたら範囲を考える」と同様に、「文字を消去するときは範囲を引き継ぐ」を意識してください。

$X$ の範囲を $Y$ の範囲にしっかりと引き継ぐのです。

$X=4-2Y$ なので、

$X>0$ より

$4-2Y>0$

つまり、

$Y<2$ となる。

$Y>0$ と合わせて

$0<Y<2$

「

0 < Y < 2

$0<Y<2$ のとき、

4 (2 - Y) Y

$4(2-Y)Y$ の最大値を求めよ」となりました。

あとは平方完成…

$4(2-Y)Y=-4(Y-1)^{2}+4$

こんなグラフ…

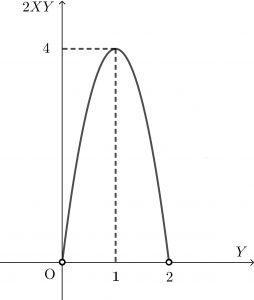
よって

$Y=1$

つまり $\log_{2}y=1$

$y=2$ で最大値 $4$ をとる。

このときの

x

$x$ の値は何ですか？

X = 4 - 2 Y

$X=4-2Y$ なので、

$X=4-2\cdot1=2$

$\log_{2}x=2$ …

つまり $x=1$ です！

解法2　まず1文字消去

$xy^{2}=16$ より、

$x=\dfrac{16}{y^{2}}$

として、 $x$ を消去してしまってもいいでしょう。

$\log_{2}y=Y$ とおいて、

$\begin{align*}(\log_{2}x^{2})(\log_{2}y) & =(2\log_{2}x)(\log_{2}y)\\& =2\left(\log_{2}\dfrac{16}{y^{2}}\right)(\log_{2}y)\\& =2(\log_{2}16-2\log_{2}y)(\log_{2}y)\\& =2(4-2Y)Y\end{align*}$

と変形できます。

ただし、文字を消去するときには範囲を引き継ぐので、

$x=\dfrac{16}{y^{2}}>1$

$16>y^{2}$

これを解いて

$-4<y<4$

これと $y>1$ より

$1<y<4$

よって

$0<\log_{2}y<2$

つまり

$0<Y<2$

あとは解法1と同じですね！

答案

解法1での答案を書いておきます。

$x>1,y>1$ において、

$\log_{2}x=X, \log_{2}y=Y$ と置くと

$(\log_{2}x^{2})(\log_{2}y)=(2\log_{2}x)(\log_{2}y)=2XY$

となる。ここで

$xy^{2}=16$ の両辺を底を $2$ とする対数をとると、

$\log_{2}xy^{2}=\log_{2}16$

$\log_{2}x+2\log_{2}y=4$

よって

$X+2Y=4$

と書き換えられる。

また $x>1$ より

$X=\log_{2}x>\log_{2}1=0$ から $X>0$

$y>1$ より

$Y=\log_{2}y>\log_{2}1=0$ から $Y>0$

ここで

$X+2Y=4$ より $X=4-2Y$

$X>0$ より $4-2Y>0$

つまり、 $Y<2$ となる。

$Y>0$ と合わせて $0<Y<2$

よって

$2XY=2(4-2Y)Y$

$\hspace{2.4em}=4(2-Y)Y$

$\hspace{2.4em}=-4(Y-1)^{2}+4　(0<Y<2)$

より

$Y=1$ ,つまり $\log_{2}y=1$

$y=2$ で最大値をとる。

このとき、

$X=4-2\cdot1=2$

$\log_{2}x=2$ つまり $x=1$

以上より、

$x=1,y=2$ で最大値 $4$ をとる。

問題

解法1 まず置換え

解法2 まず1文字消去

答案

極大値と極小値の差

二項定理・分数式の計算練習

三角関数の不等式（合成の利用）

次数下げによる極値計算

共通接線の方程式

三角関数の不等式（因数分解を利用）

解法1　まず置換え

解法2　まず1文字消去