次数下げによる極値計算
※スマホの場合、横向きを推奨

次の問題を解いてみてください。
ちょっとした罠が仕掛けてあります。
問題
$f(x)=2x^{3}+9x^{2}-6x$ の極小値を求めよ。











極値をとる $x$ の値を求める











$f'(x)=6x^{2}+18x-6$











$x=\dfrac{-3\pm\sqrt{13}}{2}$








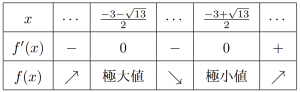









だから極小値は…
$f\left(\dfrac{-3+\sqrt{13}}{2}\right)$$=2\left(\dfrac{-3+\sqrt{13}}{2}\right)^{3}+9\left(\dfrac{-3+\sqrt{13}}{2}\right)^{2}-6\left(\dfrac{-3+\sqrt{13}}{2}\right)$








代入計算の工夫






























計算ミスを防ぐために、ここでは次数下げの方法を利用しましょう。




















$$f(x)=2x^{3}+9x^{2}-6x$$












代わりに、$f'(x)$↓に代入ならどうですか?
$$f'(x)=6x^{2}+18x-6$$








2次式なので、ちょっと楽ではありますけど…












$x=\dfrac{-3+\sqrt{13}}{2}$ は、極値をとる $x$ ですよ。導関数の値はどうなりますか?



















$f’\left(\dfrac{-3+\sqrt{13}}{2}\right)$
$=6\left(\dfrac{-3+\sqrt{13}}{2}\right)^{2}+18\left(\dfrac{-3+\sqrt{13}}{2}\right)-6$
$=0$























結果は0と分かっているんですね!












さらに、$f'(x)$ を $6$ で割った $x^{2}+3x-1$ に入れても $0$ であることも分かりますね。
割り算による変形




















$x^{2}+3x-1$ が式の中にでてきて欲しいわけですから、
$2x^{3}+9x^{2}-6x$ を $x^{2}+3x-1$ で割って…













































$2x^{3}+9x^{2}-6x$ を $x^{2}+3x-1$ で割ると、
商が $2x+3$ 、余りが $-13x+3$ です!












$$f(x)=(x^{2}+3x-1)(2x+3)-13x+3$$
余りへの代入











$f\left(\dfrac{-3+\sqrt{13}}{2}\right) $
$=-13\left(\dfrac{-3+\sqrt{13}}{2}\right)+3$
$=\dfrac{45}{2}-\dfrac{13\sqrt{13}}{2}$

















