三角関数の公式(定義から)
三角比の定義を2種類紹介しましょう。
その定義に基づいて、重要な公式を導きます。
三角比の定義
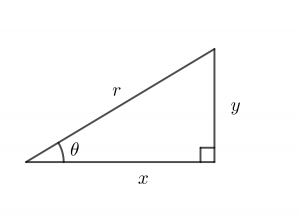
上の図において、三角比は次のように定義されます。
$\sin\theta=\dfrac{y}{r}$
$\cos\theta=\dfrac{x}{r}$
$\tan\theta=\dfrac{y}{x}$
(このとき、$\tan\theta$ は斜辺の傾きである)

三角比の定義(拡張)
上の定義では、角を一つに決めても三角形の大きさは無数にあり得ます。
しかし三角比は $\sin\theta=\dfrac{y}{r}$ のように辺の長さの比で定義されているので、三角形を拡大・縮小しても変わることはありません。
ということは三角形の大きさは扱いやすい大きさに自由に決めてしまっても構わないということです。
そこで $r=1$ であったとして考えてみましょう。
下の図のようになります。
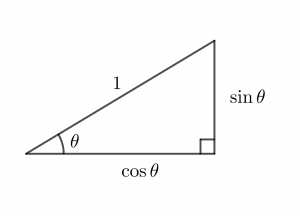








































































さて、$r=1$ としたのは、直角三角形の斜辺を半径1の円の半径としたことに対応します。
つまり下の図のように直角三角形が単位円にぴったりと収まるのです。
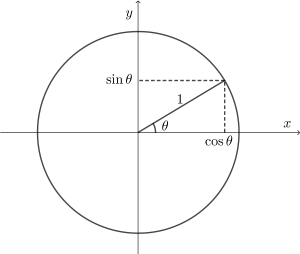



























上の図では、
$\sin\theta$ が $y$ 座標
$\cos\theta$ が $x$ 座標
になっています。
($\tan\theta$ が傾きであるのは同じです。)
これを定義とすれば直角三角形を作らずとも半径さえあればいいので、90°以上であっても、180°を超えても $\sin\theta$,$\cos\theta$ を定義できます。
上の単位円の図において、
$\sin\theta$ は $y$ 座標
$\cos\theta$ は $x$ 座標
$\tan\theta$ は半径の傾き


































これも定義なんです。
(これ以降、180°以下の角の三角比として考えず、負の角や180°を超えた角も含めた一般角の三角関数として $\sin\theta$,$\cos\theta$ をとらえることにします。)
2種類の定義


































2つの定義が同じ意味で、矛盾がなければ大丈夫です。
例えば、
定義1 「3辺の長さがすべて等しい三角形を正三角形という」
定義2 「3つの角の大きさがすべて等しい三角形を正三角形という」


























このいずれを定義としても同じであるようにです。








三角比と三角関数の違い




































定義の仕方は変わりませんが、注目していることが違いますね。
三角比は図形的な意味に注目し、三角関数は数に注目しています。
図形的性質を考える場合は180°を超えることはないです。2つの線分のなす角は最大で180°ですからね。



































一方、三角関数はどんな角に対しても定義されます。図形的意味をはぎ取るので、何回転でもしてよいのです。
そして、三角比は「長さの比」という意味を持っていますが、三角関数は数そのものです。








じゃあ意味を持たない…?
って、役に立つんですか?


























確かに、目に見えるような場面で役に立っているのは三角比の方ですね。
しかし図形的意味から脱却して、関数として考えることで色々な場面で登場するツールになるんです。
今は応用例をあまり知らないので価値を感じないでしょうが、使っていけばそのうち有難みは分かるようになると思います。






































































まずは数学Ⅲの勉強を頑張るところからですね。深い理解をしようとすると、どうしても準備に忍耐が必要になるものです。




































音楽ファイルを保存するときに、ファイルのサイズを小さくしているのは三角関数による近似ですよ。










三角関数の相互関係


























(単位円の方の図でも直角三角形が含まれていますから、単位円の図で考えても同じことです。)


公式① $\sin^{2}\theta+\cos^{2}\theta=1$
公式② $\tan\theta=\dfrac{\sin\theta}{\cos\theta}$
公式③ $1+\tan^{2}\theta=\dfrac{1}{\cos^{2}\theta}$


























公式①


































えっと、
$\sin^{2}x+\cos^{2}x=1$
…あ、できた…
公式②



































傾きは($y$ の変化量)÷($x$ の変化量)…
つまり $\dfrac{\sin\theta}{\cos\theta}$
あ、これもできた…(そのまんま…)
公式③



































$\dfrac{\sin^{2}\theta}{\cos^{2}\theta}+1=\dfrac{1}{\cos^{2}\theta}$
となるから…




































…ああ、できましたね。
公式③について
































































































数Ⅲの積分ではめちゃ使いますよ。
そのうち出てくるので、ふんわりでいいので覚えておいてください。
三角関数の変換
三角関数の定義から、次の公式を作ることもできます。
$\sin(90°-\theta)=\cos\theta$
$\cos(90°-\theta)=\sin\theta$
$\sin(180°-\theta)=\sin\theta$
$\cos(180°-\theta)=-\cos\theta$
$\sin(-\theta)=-\sin\theta$
$\cos(-\theta)=\cos\theta$
$\sin(90°+\theta)=\cos\theta$
$\cos(90°+\theta)=-\sin\theta$










ちょ、こんなにたくさん覚えられないです…
どれもよく似てて紛らわしいし…


























これは覚えるものではなく、作るものです。
図形的に考えればすぐに分かることです。
例1
具体的な例として、$\sin(-20°)$ について考えてみましょう。
$-20°$ は、下の図の青い部分になります。
ところで、$20°$ を考えると赤い部分になりますから、
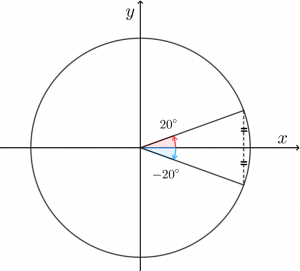

$-20°$と$20°$は上下対称となり、 $\sin(-20°)$ と $\sin20°$ は大きさが同じで向きが逆になります。よって、
$\sin(-20°)=-\sin20°$
が言えます。
一般化
同じように考えて、(図の20°のところを $\theta$ に差し替えて)
$\sin(-\theta)=-\sin\theta$
が分かります。
例2
$\sin160°$ の値について考えてみましょう。
20°を考えてみると、赤い部分になります。
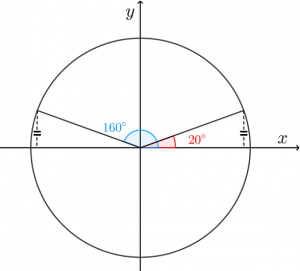




































対称になるように角度を選んだんです。
ここでは、左右対称になるように、180°から160°を引いた20°を考えました。
すると、160°と20°は高さが等しいと分かり、
$\sin160°=\sin20°$
が言えます。
一般化
同様に考えて、
$\sin(180°-\theta)=\sin\theta$
が言えます。




































図の20°のところを $\theta$, 160°のところを$180°-\theta$ と差し替えて考えてみてください。
例3
$\cos110°$ はどうでしょう。
20°は赤い部分になります。(今度は90°差の角を取りました)
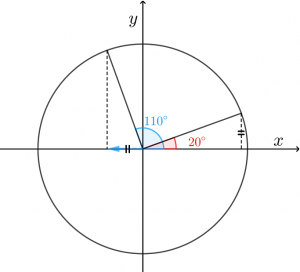




































合同ですね。
$\cos110°$ は青い矢印です(左向きなので、負の値)。それと同じ長さの辺が見つかりますか?









赤の三角形の高さ($\sin20°$)と同じです!
正負に気を付けて、
$\cos110°=-\sin20°$
一般化
110°のところを$90°+\theta$,20°のところを $\theta$ と差し替えて、
$\cos(90°+\theta)=-\sin\theta$
が言えます。






