$0≦\theta<2\pi$とする。
$$\sqrt{2}\sin2\theta-2\sin\theta-\sqrt{2}\cos\theta+1>0$$
方針
どこから手を付けたらいいのでしょうか…
例えば不等式 $x^2-x<0$ を解けと言われたら、まずはどんな変形をしますか？
2倍角の公式の利用と因数分解
まず2倍角の公式を使って、与式を
$2\sqrt{2}\sin\theta\cos\theta-2\sin\theta-\sqrt{2}\cos\theta+1>0$
と変形しました。これを因数分解はできますか？
$2\sin\theta(\sqrt{2}\cos\theta-1)-\sqrt{2}\cos\theta+1>0$
共通因数がありますね！
$\sqrt{2}\cos\theta-1$ が共通因数です！
$2\sin\theta(\sqrt{2}\cos\theta-1)-(\sqrt{2}\cos\theta-1)>0$
$(2\sin\theta-1)(\sqrt{2}\cos\theta-1)>0$
OKです。「1文字について整理する」因数分解をしたんですね。（この場合 $\sin\theta$ に注目）
不等式の表す領域を考える
$(2\sin\theta-1)(\sqrt{2}\cos\theta-1)>0$
「不等式の表す領域」のことは覚えていますか？
今解いている問題はいったん置いておいて、例えばですが…
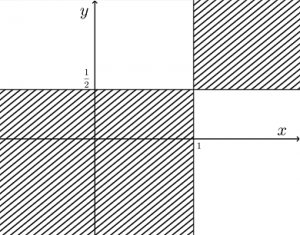
$(x-1)(2y-1)>0$
の表す領域はどのようになりますか？
$\begin{cases}x-1>0\\2y-1>0\end{cases}$
または
$\begin{cases}x-1<0\\2y-1<0\end{cases}$
$\begin{cases}x>1\\y>\dfrac{1}{2}\end{cases}$
または
$\begin{cases}x<1\\y<\dfrac{1}{2}\end{cases}$
$(2\sin\theta-1)(\sqrt{2}\cos\theta-1)>0$
この不等式が表す領域を図示するイメージで解いたらいいということですね！
$2\sin\theta-1＝0$ ($\sin x=\dfrac{1}{2}$ の横線）と
$\sqrt{2}\cos\theta-1＝0$（$\cos x=\dfrac{1}{\sqrt{2}}$の縦線）
を境界線とする領域をかけばよいのです。
$\begin{cases}2\sin\theta-1>0\\\sqrt{2}\cos\theta-1>0\end{cases}$
または
$\begin{cases}2\sin\theta-1<0\\\sqrt{2}\cos\theta-1<0\end{cases}$
$\begin{cases}\sin\theta>\dfrac{1}{2}\\\cos\theta>\dfrac{1}{\sqrt{2}}\end{cases}$
または
$\begin{cases}\sin\theta<\dfrac{1}{2}\\\cos\theta<\dfrac{1}{\sqrt{2}}\end{cases}$
ということは、図の右上と左下…
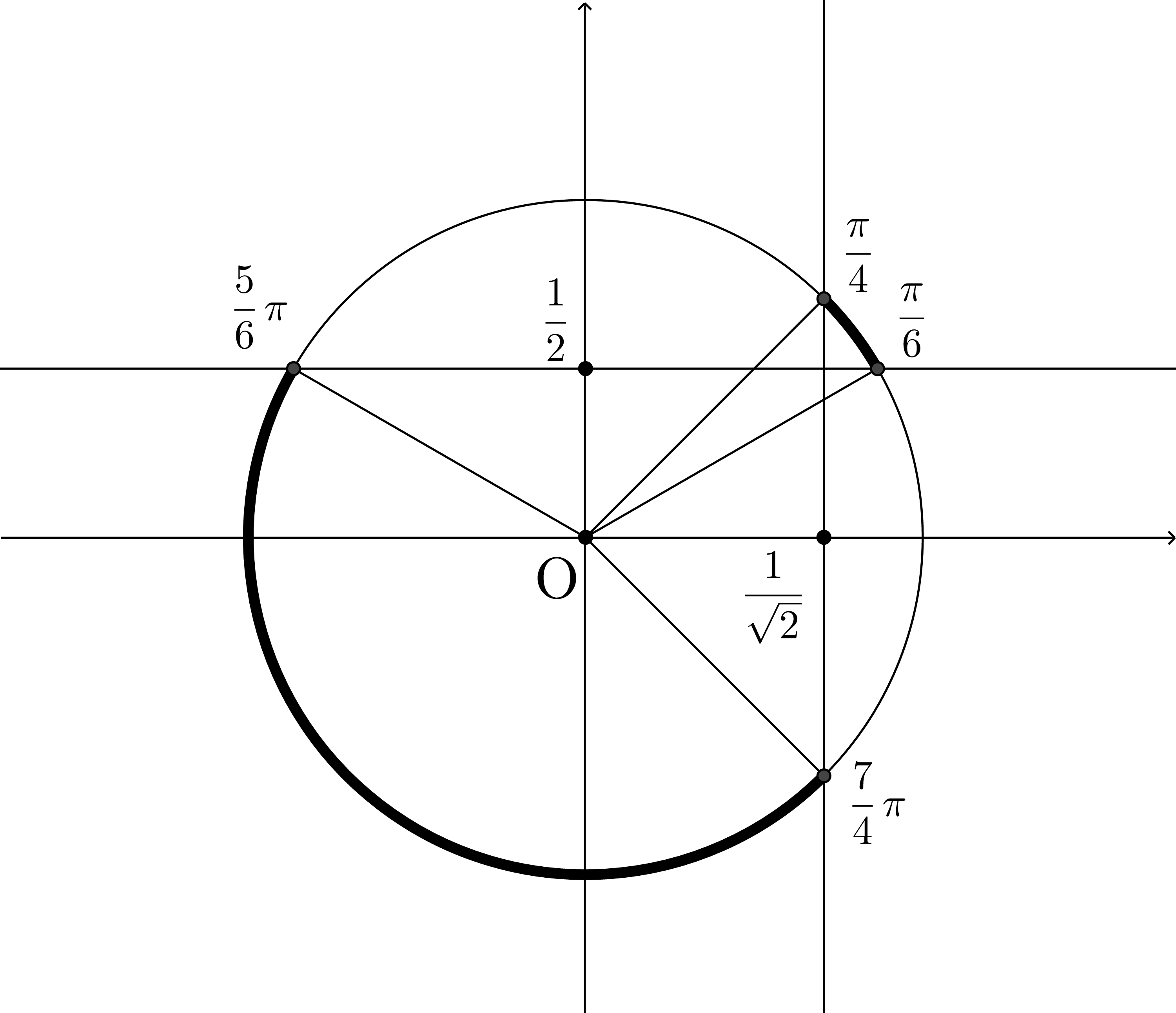
求める $\theta$ の範囲は
$\dfrac{\pi}{6}<\theta<\dfrac{\pi}{4} , \dfrac{5}{6}\pi<\theta<\dfrac{7}{4}\pi$ …（解答終わり）
