3次関数のグラフに3本の接線が引ける条件
微分についての様々な操作が盛り込まれた問題なので、微分を学びはじめた人にとって確実に力になる問題です。
曲線 $y=x^{3}-3x-5$ に $(1,a)$ から異なる $3$ 本の接線が引けるような定数 $a$ の値の範囲を求めよ。
「接点 $t$」での接線
$y’=3x^{2}-3$ より
$(t,t^{3}-3t-5)$ における接線の式は
$y-(t^{3}-3t-5)=(3t^{2}-3)(x-t)$
これを整理すると
$y=(3t^{2}-3)x-2t^{3}-5$
とかける。
なぜ接点 $t$ か
この問題は、接点の座標が与えられていない問題です。与えられた点 $(1,a)$ は接点ではなく、ただの通る点です。
（たまたま接点にもなっていることはあるかもしれませんが。）
よってその $x$ 座標に当面の名前を与えないといけません。それを $t$ としたのです。
通る点の代入
$y=(3t^{2}-3)x-2t^{3}-5$
と表せました。問題文の中で、まだ使っていない条件がありますね？
$(1,a)$ を通るので…
$a=(3t^{2}-3)-2t^{3}-5$
$a=-2t^{3}+3t^{2}-8$
ここで $a$ が具体的な数であればあとは $3$ 次方程式をといて、仮に出てきた実数解が1つだけなら、その解を
$y=(3t^{2}-3)x-2t^{3}-5$
に戻せば接線の方程式が1つだけ出てきます。
実数解の個数が2個なら接線の方程式は2つで…
「方程式 $a=-2t^{3}+3t^{2}-8$ が異なる3つの実数解を持つ」
と言い換えられます。
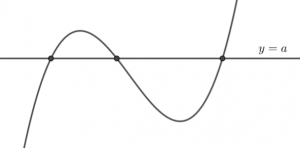
この場合、$a$ が単独で左辺に存在しているので、このまま左辺に寄せておくのが解きやすいです。
「定数分離」という考え方です。
きいたことあります！
実数解の個数
$f(t)=-2t^{3}+3t^{2}-8$ とすると、導関数は
$f'(t) =-6t^{2}+6t$
$\hspace{2.25em}=-6t(t-1)$
よって $f(t)$ の増減表は次のようです。
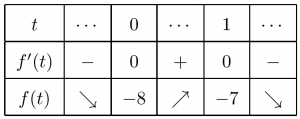
よって求める $a$ の値の範囲は
$$-8<a<-7$$
答案
$y’=3x^{2}-3$ より
$(t,t^{3}-3t-5)$ における接線の式は
$y-(t^{3}-3t-5)=(3t^{2}-3)(x-t)$
これが $(1,a)$ を通るとき
$a-(t^{3}-3t-5)=(3t^{2}-3)(1-t)$
すなわち
$a=-2t^{3}+3t^{2}-8$
が成立する。これを満たす $t$ の値が3つ存在することが条件であるから
$f(t)=-2t^{3}+3t^{2}-8$
として
$f'(t) =-6t^{2}+6t$
$\hspace{2.25em}=-6t(t-1)$
よって $f(t)$ の増減は次のよう。
よって求める $a$ の値の範囲は
$-8<a<-7$
